Mr. Oragahn wrote:Schrodinger82 wrote:You're still going on about the blue star incident?
I was just watching a special about the Sun on the History channel. One of the things they discussed was how it was that the coronas can be heated up to such a high degree, despite being so far away from the sun. You know what one leading theory is?
Sonic energy.
Apparently, the turbulant forces that go on at the surface of the sun act as a giant convection engine, which produces massive quantitees of sound. The entire sun basically acts as a celestial loud speaker, loud energy so that the sound waves are capable of superheating the plasma to millions of degrees.
And yet in the episode, the blue star was pretty much silent. Thereby suggesting that the ship was much, much, much further away then you would care to admit.
Being able to understand Disney Channel is one thing.
Comprehending that what you say is completely irrelevant to the matter at hand is another thing.
The calculation was never based on how hot the corona was. It was solely based on the energy radiated by the sun from the photosphere.
Besides, having the corona being very hot doesn't mean that it will make plasma radiate much light. Gas densities in coronas are very low. With no noticeable luminosity that is worth it, it's pointless to make calcs based on the heat of the corona.
What we know is that, in terms of plot, Jacob only went close enough to the sun in order to throw off the Ha'tak sensors. There would be absolutely no reason for him to go and closer than that, especially since his goal was to attain maximum shield life, rather than to get as close to the sun as possible for the sake of fanwank generating fanwank.
I didn't claim they got into the chromosphere, nor in the photosphere, as far as I'm concerned.
This is also ignoring the fact that there's a big difference between relative distance and actual distance, and that you can't reliably calculate how far the Ha'tak is from the sun based solely on their relative size, assuming that you actually did know their relative size, because you would need to know where the position of the observer is relative to either object (Which you don't). It also ignores the fact that the FX designers intended to render the event to scale, which means that the scale would be a usable frame of reference, which would not only require the writers to explicitly type out the calculations, but which would also require that the FX people would have the computing power to render it (Since the scale between the star to the ship would be over 1000000 to one, which means that the star would require 1000000 times as many pixels.).
Edit: The current assumption is that we see a picture of object X standing in front of object Y, and we know the size of X and Y, then we can calculate their distance by comparing their actual sizes to their apparent sizes. There's a problem with that assumption:

Let's say that I tell you how tall the actors are, and how wide that sign in the background is. Can you tell me exactly how far away the actors are from the sign based solely off of that, and come up with the exact same numbers for every frame? If not, then the whole idea that you can calculate distance is somewhat questionable.
What matters is to know that why
on screen, the sun and the ha'tak look in a given way. Based on their known dimensions - smallest dimensions for a blue giant, and smallest dimensions for a ha'tak - we can then work from camera angular values. Tight angles give a weak perspective, while wide angles seem to cram everything in, and give the fisheye effect.
- Wide angle : short focus lenght : towards fish eye effect. Objects seem distant. Small and distant objects in the background appear extremely small.
- Tight angle : long focus lenght : towards perspective less view. Objects seem to be crammed in front of the eye lens. Small and distant objects in the background appear bigger.
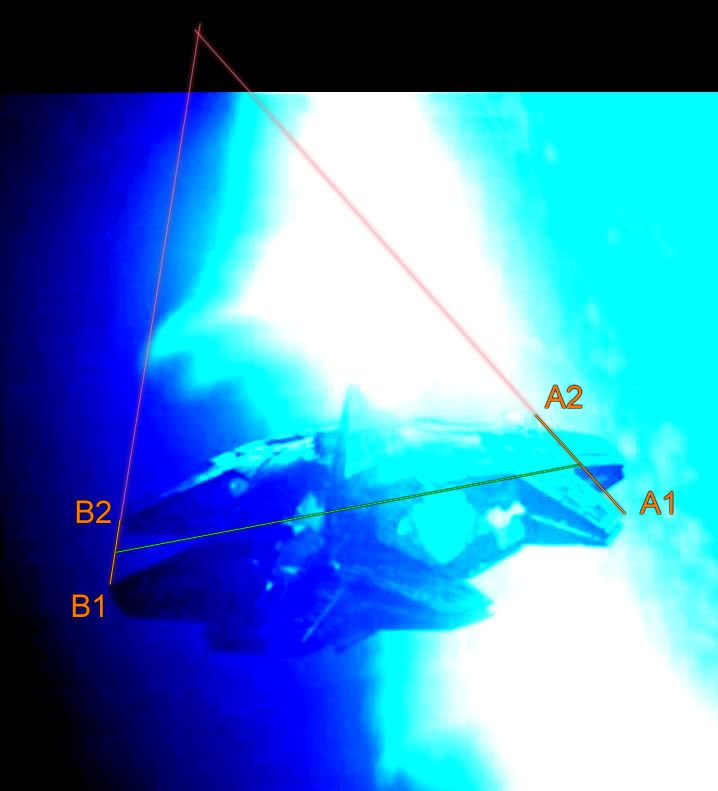
Let's try to gauge the amount of perspective present in
this picture.
Where can we draw parallel lines through the ha'tak's structure?
Well, this one is easy. See below:
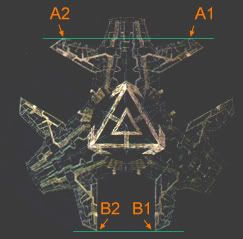
Now let's find those lines in the screencap:
So I went into max and tried to emulate this image.
I Put a cone with three sides plus a base, surrounded it with a rectangle which most distances and opposite sides would have edges which would point towards the horizon, like the lines drawn between A1, A2, B1 and B2.
Then, I placed a blue sphere. A small one, at a far distance, and played with the camera's focal lenght.
The highest standard value offered in max for the local lenght is 200 mm. It corresponds to a field of vision (FOV) of 10.286 degrees.
There are zero chances that the artist made the scene to scale. The blue giant was probably only a couple of times wider than the ha'tak model. If they even rendered all the elements in the same scene.
What matters most here is to know how much subject to perspective the ha'tak is. Remember, your argument is that we can't know the FOV, and thus a small one (high focal lenght) would make a distant and small sphere appear extremely big.
Here's a view of the rectangle, with the pyramid core placed in its center:

As you see, the most distant edges of the rectangle's sides are roughly as distant as the A and B lines are to each other, and all are parallel.
Now, let's see what it looks like when seen from a camera with an absurd focal lenght of 1355 mm:

Everything seems fine. The pyramid is oriented in a similar way, the blue giant horizon seems as flat and big as on the screencap.
However, there's a big problem. The distance between the A and B points is completely lost. We can't see the parallel edges anymore.
Which proves that, at least, the focal lenght is not that high.
So let's go directly down to a 200 mm long one, and see what it looks like on the camera:

As you notice, when fiddling with the focal lenght, you have to pan the camera back and forth in order to keep your subject within the same screen proportions.
So in this case, I need to bring the camera closer to the pyramid.
I won't scale the objects up or down.

However, there's another problem.
In the former renderings, the back of the rectangle (the side not facing the camera) has its normal (line perpendicular to the face) pointing to a location out of the screen,
much like in the episode's cap. Everything was OK.
But on making the focal lenght shorter, this normal now points to a point that is located behind the rectangle, so I have to rotate the rectangle to have its edges point in a similar fashion as the A and B lines do.
I'll also cut the rectangle, so there will be a ring of new edges, where the backface's perimeter was, before I pushed it into the distance. So these new edges form a ring that parralel to the front face. That way, we see both where the edges point to, and the original pyramid-scaffoling initial rectangle shape:

As we can see, even with a much shorter focal lenght of 200 mm, the side edges are still too small. They're twice as short as the B line (the shortest one).
Remember that the rectangle encompassed the pyramid. The B line, however, is shorter than the pyramid's max width. With this in mind, look at the rendering with now a focal lenght of 85 mm (slightly below 24°):

The sphere nonwithstanding, as we can see, the perspective on the rectangle starts to look like what we have in the screencap.
We get relatively sizeable side edges. Look at the whitened edge; it's nearly as big as the B line.
And now, I'll make the sphere very big, and move it around, to make it look like as big as in the screencap:
 Conclusion:
Conclusion:
The focal lenght can't be absurdly high, and would start at 80 mm, if not below. It would not surprise me that they used one in that ballpark. Even the differences with a 50 mm one are minimal, and still look episode-like, and there's enough room between approximations in the positions and dimensions of the objects to actually reach even shorter focal lenghts.
It's also very possible that they didn't use a whole sphere, but just a portion and pasted the neat sun flare effect on it. Which would then make it even more pointless to fiddle with focal lenghts, as they'd just need to make a slightly curved patch.
Point being that the blue giant looked big because they were close to it.
Now, I was planning redoing all the calcs from the beginning, much more detailed and intricate than any calculation done by anyone else.
I'd use the following dimensions, as far as the Goa'uld ship and the blue giants are concerned:
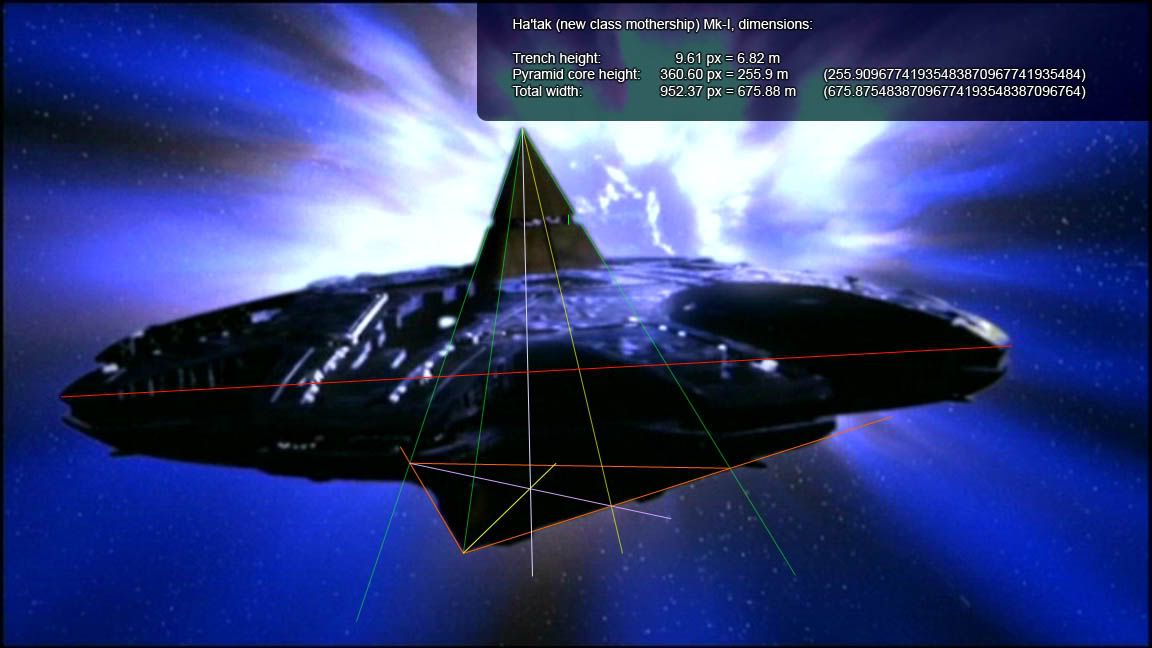
I did measurements for Ha'taks Mk-I which gave me a width of 675 meters. The Mk-II, introduced around season 4 by Sokar if I'm correct, always seemed larger. I've seen figures giving the new ones widths between 700 meters and 725 meters.
So I'll use a 700 m width.
As far as the blue giant is concerned, I'll work from the smallest typical blue giant, from the B class. That's a sun 7 times wider than Sol.
So that's D = 1.392 e9 x 7 = 9.744 e9 m.
The hardest part is to gauge the curvature of the sun's horizon.
A low end figure will require a very curved horizon, which means a great distance between the ship and the sun. A near flat horizon will mean that the ha'tak was closer to the sun.
If you're going to make the assertion that the shields are literally billions of times more powerful than actual concrete examples would suggest, then you would need something a bit more substantive. Because right now, the "calculations" you've presented are full of holes and contradictions.
Says the guy who claims that Sateda's extremely sub kiloton explosions were the be and end all of Wraith hiveship's firepower.
I'm not responding to you because your argument is new or anything. It's the same old, rehashed and debunked stuff. I'm doing it because I don't want to see people get misinformed because of your erroneous claims.
We simply know that you just have a big problem with facts and numbers. So be it if they're big, since even small quantities of naqahdah do generate huge amounts of power.
These are the concrete examples.
SHEPPARD: Hold on – we’re just gonna tap on the brakes here. (He pulls a lever back and he and Rodney shoot forward in their seats as the F-302 decelerates rapidly. The virus ship flashes past underneath them. Rodney gulps, trying not to be sick. In Engineering, Elizabeth and Hermiod watch the ships change position.)
WEIR: Nice move!
HERMIOD: Indeed.
SHEPPARD: He’s making a break for the chromosphere.
McKAY: Would it be good to mention that we have less protection in this ship than we did on the Daedalus?
SHEPPARD: Not really.
McKAY: I didn’t think so.
(John’s ship chases the virus ship towards the sun.)
HERMIOD: Radiation levels in the Colonel’s ship are beginning to rise.
(In John’s ship, the sun is shining directly into the cockpit.)
McKAY: Is it just me, or is it getting a little hot in here?
(In Engineering, the ships disappear from the screen.)
WEIR: What happened?
HERMIOD: They are approaching the chromosphere. There is too much interference.
(In John’s ship, Rodney is shielding his eyes from the sun.)
McKAY: The thing is, I have very fair skin. I tend to burn easily.
SHEPPARD: Just a few more seconds. (He looks at his control screen. The screen fritzes for a moment, but then comes back, and then the virus ship is in the centre of the screen and a target lock is shown. John fires a missile, which flies towards the virus ship and blows it to bits.)
Lookie there. Sheppard and McKay, in a perfectly normal and completely unshielded 302, manage to fly into the chromosphere of a star (Which is closer to the star than the corona), close enough to interfere with the sensors (As Jacob did to the enemy ships), and still managed to walk away with no ill effects.
That must mean that McKay must be uber tough. It also means that any time we've seen him shot, the weapon that shot him must have been in the multi-GT range, in order to have enough firepower to penetrate his skin.
Oh my god. That is just so full of errors, I don't know where to start from.
First, when you claim that Jacob placed the ha'tak inside the chromosphere of a
blue giant. Clue: Yes, they'd fry instantly that close to a blue giant, even a low class one.
That said, it's critically higher than any claim I, and other people who made calcs, have made about the distance between the blue giant and the ha'tak. I claim the ha'tak is the corona, at a certain distance from the sun. Not in the chromosphere.
Fact being, anyone who had seen the episode would know that anyone claiming that the ha'tak was inside the chromosphere can't be taken seriously:

Secondly, they were
approaching the chromosphere of a yellow sun, a G class main sequence star, just like our sun. It is considerably less luminous than a blue giant.
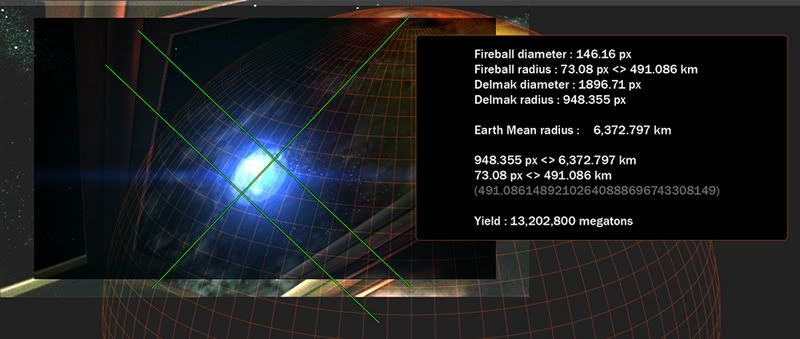
Blue giants are either O or B. The weakest B class average luminosity is already 20,000 times Sol's, and can reach, for the highest values, 1.4 e6 times the Sol's.
The sun has a mean diameter of 1.392 e9 m. The averaged G star is 10% wider than our sun.
So that's D = 1.392 e9 x 1.1 = 1.5312 e9 m.
Or a radius of 0.7656 e9 m.
Sol has a luminosity of 3.846 e26 W.
Thus, the intensity at the photosphere is:
I = 3.846 e26 / 4 x pi x (0.7656 e9)²
I = 52,215,034.14 W/m²
I = 52.21503414 megawatts/m².
I = 12.48 kg of TNT per second, per unit of surface area (m²).
That is at the photosphere, for an average G class star.
They were not even there. Not even
in the chromosphere. They were
approaching it, which can mean anywhere from
inside the corona, and likely still at a safe distance.